[ad_1]
Neural language models (LMs) have become popular due to their extensive theoretical work mostly focusing on representational capacity. An earlier study of representational capacity using Boolean sequential models helps in a proper understanding of its lower and upper bound and the potential of the transformer architecture. LMs have become the backbone of many NLP tasks, and most state-of-the-art LMs are based on transformer architecture. In addition, formal models of computation offer a smooth and accurate formulation to study different aspects of probability distributions that LMs can handle.
However, LM architecture is mostly examined in the context of binary language recognition, which creates a category error between LM (distribution over strings) and theoretical abstraction (a set of strings). To solve this issue, it is important to figure out the classes of probability distributions over strings represented by the transformer. Moreover, the analysis of architecture for language acceptance is the major area of focus for most researchers. However, researchers of this paper argue that this is not the optimal approach to solving such a problem in the field of LMs, which are probability distributions over strings.
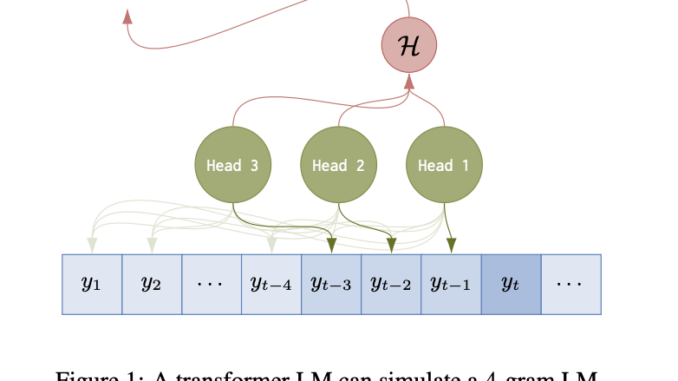
Researchers from ETH Zurich studied the representative capacity of transformer LMs with n-gram LMs. They successfully demonstrated that it is easy to capture the parallelizable nature of n-gram LMs with the help of transformer architecture, offering various lower bounds on the probabilistic representational capacity of transformer LMs. These transformer LMs consist of multiple transformer layers and represent n-gram LMs using hard and sparse attention, showcasing various ways transformer LMs can simulate n-gram LMs. It utilizes the attention mechanism to enhance the input representations, including queries, keys, and values, by evaluating their updated versions.
Researchers gave two theorems to explain the representative capacity of hard attention transformer LMs. The first theorem states that, for any n-gram LM, there exists a weakly equivalent single-layer hard attention trans former LM with n – 1 head. Its proof intuition is that a weakly equivalent LM defined by a transformer is constructed that looks back at the preceding n – 1 positions using n – 1 heads. The second theorem states that, for any n-gram LM, there exists a weakly equivalent n – 1-layer hard attention trans former LM with a single head. Its proof intuition is that an n – 1 layer transformer LM can use the n – 1 layers to look back at the immediately preceding position and copy it forward n – 1 times.
Transformer LMs and traditional LMs are connected to capture any n-gram LM using the method of hard and sparse attention transformer LMs, which provides a stable lower bound on their probabilistic representational capacity. Moreover, the role of several heads and the number of layers consists of a balance between the number of heads, layers, and the complexity of the non-linear transformations required to simulate n-gram LMs. Overall, these results contribute to the probabilistic representational capacity of transformer LMs and the mechanisms they might utilize to execute formal computational models.
In conclusion, Researchers from ETHzurich studied the representative capacity of transformer LMs with n-gram LMs, capturing the parallelizable nature of n-gram LMs using the transformer architecture and providing multiple lower bounds. Researchers showed that transformer LMs can represent n-gram LMs using hard and sparse attention, demonstrating various mechanisms they can utilize to present n-gram LMs. However, some limitations have been highlighted for future work: n-gram LMs represent a very simple class of LMs, resulting in loose lower bounds, making the transformer LMs exhibit a more complex structure than n-gram LMs.
Check out the Paper. All credit for this research goes to the researchers of this project. Also, don’t forget to follow us on Twitter. Join our Telegram Channel, Discord Channel, and LinkedIn Group.
If you like our work, you will love our newsletter..
Don’t Forget to join our 40k+ ML SubReddit

Sajjad Ansari is a final year undergraduate from IIT Kharagpur. As a Tech enthusiast, he delves into the practical applications of AI with a focus on understanding the impact of AI technologies and their real-world implications. He aims to articulate complex AI concepts in a clear and accessible manner.
[ad_2]
Source link





Be the first to comment